Vocab

  • heuristic solution: an approach to a problem that produces a solution that isn’t necessarily optimal but can be used when normal methods to an optimal solution would take forever
  • algorithmic efficiency: The ability of an algorithm to solve a problem in an efficient way
  • decidable problem: problem in cs and mathematics for which an algo can be created that can always produce a correct answer
  • undecidable problem: problem in cs and mathematics for which it is impossible to create an algorithm that can always provide a correct answer or solution.

Algorithm Efficiency and Undecidable Problems

  • algorithmic efficiency
    • The ability of an algorithm to solve a problem in an efficient way
    • An efficient algorithm solves a problem quickly and with a min amount of resources, such as time and memory.
  • How do we determine if an algorithm is efficient or not?
    • One way we can do this is by determining the time complexity of the algorithm.
    • Another way is through space complexity.
  • Time complexity
    • How does the runtime of the function grow as the size of the input grows

array = [1, 5, 8, 3 …, 10]

def find_sum(array): total = 0 for each i in given array: total += i return total

  • heuristic solution
    • an approach to a problem that produces a solution that isn’t necessarily optimal but can be used when normal methods to an optimal solution would take forever
    • Usually made up using logic
  • Traveling Merchant Problem Hacks:
    • What did you and your team discuss? (record below)
      • start at Indianapolis, then Louisville Cincinnati, Columbus, Detroit, and finally Chicago (805 miles)

travel

  • decidable problem
    • problem in cs and mathematics for which an algo can be created that can always produce a correct answer
    • there exists an algo that can be used to determine whether a given input is a valid solution or not
def divideThirteen(number):
    if number % 13 == 0:
        return True
    else:
        return False

print(divideThirteen(26))
print(divideThirteen(30))

True
False
  • undecidable problem
    • a problem in cs and mathematics for which it is impossible to create an algorithm that can always provide a correct answer or solution.
    • not possible for an algorithm to always determine whether a given input is a valid solution to an undecidable problem
i = 0
number = 1
def integerTest(n):
    # Testing if the number is an integer
    if n%1 ==0:
        return True
    else:
        return False
# Using while loop to keep searching an a non-integer above 1. Note that the computer runs forever.
while i == 0:
    number += 1
    if integerTest(number) == False:
        i +=1
        print("Done")
  • halting problem
    • example of an undecidable problem
    • no way to write an algo to analyze and determine whether a body of code can run forever or not
  • halting problem example
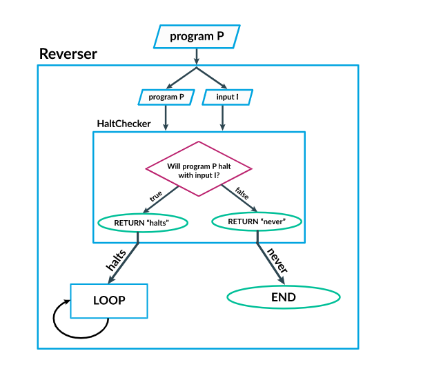
    • HaltChecker analyzes the program, program P, and its input, input I. If program P halts with input I, HaltChecker returns an output of "halts". If program P doesn't halt(runs forever) with input I, HaltChecker returns an output of "never". For example, in the code where it tests if variable number, the code runs forever, so HaltChecker returns an output of “never”.
    • Then, we add another algorithm called Reverser which reverses HaltChecker's output. So, if "never" is the output of HaltChecker, then the output of Reverser is “halts”. It's also the same the other way around: if HaltChecker has an output of "halts", then Reverser has an output of “never”.
    • We combine these algorithms into one entire body of code.
    • Since Reverser is the algorithm at the end, hence giving the ultimate output, notice how it prints "never" when in fact there is an end(As proved by HaltChecker), and how it also prints "halts" when there is in fact is no end to the code(Also proved by HaltChecker). As a result, HaltChecker is inaccurate and this is an undecidable problem

halt

HW

  • Come up with one situation in which a computer runs into an undecidable problem. Explain why it is considered an undecidable problem
    • an algorithm which finds all solutions of a Diophantine equation.
    • A Diophantine equation is a more general case of Fermat's Last Theorem; we seek the integer roots of a polynomial in any number of variables with integer coefficients. Since we have only one equation but n variables, infinitely many solutions exist in the complex plane
    • however, the problem becomes impossible if solutions are constrained to integer values only.
  • graph activity
    1. Use the 1st code below and graph it (Desmos, TI Inpire Cas, e.t.c), change the x value only!
    2. Label the number of loops done as x and the time (microseconds) to find the index as y
    3. Connect the points
    4. Do the same thing with the 2nd code
    5. Compare the two graphs and explain which one of the two is more efficient and why (min. 2 sentences)

The first graph appears to be more linear while the second graph resembles the graph of logn. The linear graph is always increasing, meaning that the bigger your number is, the longer it takes to identify your number. However, in the second graph, while the curve does increase, it increases slower than the linear one. This means that as the range of a list of numbers increases, the linear graph shows that time will increase more steeply than the graph of logn. Hence lists with more numbers will take less time for the logn graph vs the linear graph because the logn graph makes it so that time increases in very small increments. Therefore, second graph is more efficient. In addition, the points of the first graph are calculated using linear search which iterates through each number in the list one by one until it identifies the number. On the other hand, the second graph's points are calculated using binary search. Binary search cuts the list in half each time, repeating this process until your number is found. Therefore, binary search is much faster than linear search, hence the second graph is much more efficient.

Graph 1

graph1

Graph 2

graph2

import time

def linear_search(lst, x):
    start_time = time.perf_counter_ns() # records time (nanoseconds)
    for i in range(len(lst)): # loops through the entire list 

        if lst[i] == x: # until the x value we are looking for is found
            end_time = time.perf_counter_ns() # records time again
            total_time = (end_time - start_time) // 1000 # subtracts last recorded time and first recorded time
            print("Found element after {} loops in {} microseconds".format(i+1, total_time)) # prints the results
            return print("Your number was found at", i)
            
    end_time = time.perf_counter_ns() # records the time again
    total_time = (end_time - start_time) // 1000 # subtracts last recorded time and first recorded time
    print("Element not found after {} loops in {} microseconds".format(len(lst), total_time)) # prints the results
    return "Your number wasn't found :("


lst = list(range(1, 10001)) # list with numbers 1-10000

x = 10000 # replace with an integer between 1 and 10000 (I suggest big numbers like 500, 2000, so on)

linear_search(lst, x) # runs procedure

Found element after 10000 loops in 616 microseconds
Your number was found at 9999

import time 

def binary_search(lt, x):
    start_time = time.perf_counter_ns() # starts timer
    low = 0 # sets the lower side 
    mid = 0 # sets mid value
    high = len(lt) -1 # sets the higher side
    num_loops = 0 # number of loops the search undergoes to find the x value

    while low<=high: # Loop ran until mid is reached
        num_loops += 1 # adds one loop each time process is repeated
        mid = (low + high) // 2 # takes the lowest and highest possible numbers and divides by 2 and rounds to closest whole #

        if lt[mid] == x:
            end_time = time.perf_counter_ns() # records time
            total_time = (end_time - start_time) // 1000 # time in microseconds
            print("Element found after {} loops in {} microseconds".format(num_loops, total_time)) # prints the results
            return mid # returns the index value

        elif lt[mid] > x: # if mid was higher than x value, then sets new highest value as mid -1 
            high = mid -1 

        elif lt[mid] < x:
            low = mid + 1 # if mid was lower than x, sets the new low as mid + 1
            
    end_time = time.perf_counter_ns()
    total_time = (end_time - start_time) // 1000 
    print("Element not found after {} loops in {} microseconds".format(num_loops, total_time)) # prints the results
    return "Your number wasn't found :("


lt = list(range(1, 10001)) # list with numbers 1-10000

x = 100 # replace with an integer between 1 and 10000 (I suggest big numbers like 500, 2000, so on)

binary_search(lt, x) # runs procedure

Element found after 13 loops in 22 microseconds

99
  • Write an algorithm that solves a decidable problem. You can use math or whatever else you would like to do.
def isPrime(x):
    for i in (2, x-1): #each number until x
        if x % i == 0: #tests to see if the remainder is 0
            return False
    return True

isPrime(3793)

True
  • Write code to get the computer to run forever
import random
x = 1
y = x + random.randint(1, 100) #forces y to always be greater than x. aka y will never equal x

while x != y: #since x and y will never be equal, the loop never ends.
    if x < y:
        y = x - random.randint(1, 100)
    else: 
        y = x + random.randint(1, 100)